¿Qué es el algoritmo Dijkstra? 🤖
Publicado el 05.02.2023 a las 20:36
¿Qué es el algoritmo Dijkstra? 🤖
⚫ Introducción
⚫ ¿Cómo funciona el algoritmo Dijkstra?
🟣 ¿Cómo se etiquetan los nodos?
⚫ Vamos a verlo con un ejemplo
🟣 Etiquetando el nodo origen
🟣 Etiquetando el primer nivel de nodos
🟣 Etiquetando el segundo nivel de nodos
🟣 Etiquetando el tercer nivel de nodos
🟣 Etiquetando ...
🟣 Fin del algoritmo, obteniendo la ruta óptima
¿Qué es el algoritmo Dijkstra? 🤖
Introducción
Existen varias aplicaciones donde es necesario conocer el camino más corto entre 2 puntos en un grafo o mapa, y en la práctica normalmente no es la línea recta, me explico.
Cuando enciendes tu navegador y le pides que te lleve a un destino tu navegador lo calcula increíblemente rápido y te garantizo que la ruta que te propone es la mejor entre todas las posibles.
Pero... con la increíble casuística de carreteras, caminos, intersecciones... que existe ¿cómo se resuelve tan rápido?
La respuesta es con el algoritmo de Dijkstra.
El algoritmo de Dijkstra se utiliza para encontrar la ruta más corta en un grafo no negativo (todos los pesos o costos asociados a las aristas son mayores o iguales a cero).
Este algoritmo es necesario porque en muchos problemas de ruteo y camino mínimo, se requiere encontrar la ruta más eficiente desde un nodo de origen hasta un nodo de destino.
El algoritmo de Dijkstra no sólo se usa en la navegación GPS, también se usa en la red de telefonía y en la optimización de redes de transporte y logística.
Gracias al algoritmo de Dijkstra disfrutas de una conexión a internet con la menor latencia posible 😉🎮
¿Cómo funciona el algoritmo de Dijkstra?
Funciona asignando una etiqueta con puntuación (distancia) a cada nodo y luego seleccionando el nodo con la puntuación en la etiqueta más baja para visitar y actualizar las puntuaciones de las etiquetas de los nodos adyacentes.
Dicho de otra forma, el algoritmo Dijkstra utiliza una estructura de datos de cola de prioridad para mantener una lista de nodos visitados y sus distancias actualizadas. A cada iteración, se selecciona el nodo con la distancia mínima de la cola y se actualiza la distancia de sus vecinos no visitados.
Este proceso se repite hasta que se alcance el nodo destino o se compruebe que no existe una ruta válida.
¿Cómo se etiquetan los nodos?
Las etiquetas tendrán el siguiente aspecto [7,D](2), analicemos qué es cada parte:
- El primer número, en este caso el 7, indica la distancia acumulada, que es la distancia desde el nodo origen hasta el nodo en el que nos encontramos actualmente.
- La letra, en este caso, D indica el nodo del que venimos o nodo predecesor.
- El subíndice indicará el número de iteraciones entre paréntesis.
Vamos a verlo con un ejemplo
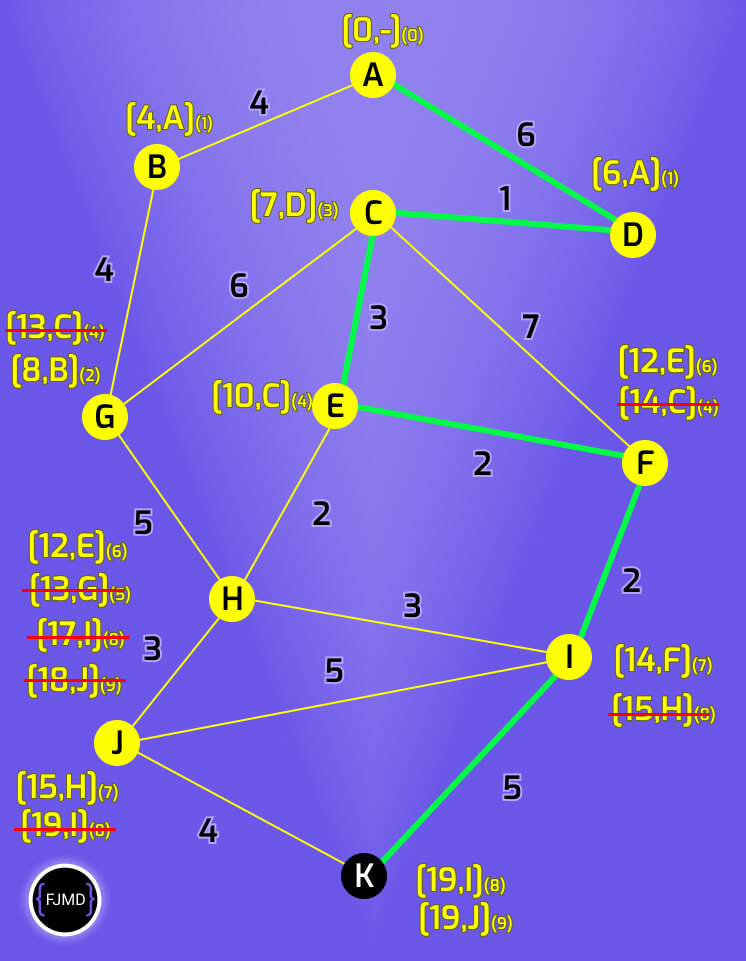
Imagina que tenemos el siguiente grafo y queremos ir del nodo A al nodo K.

Etiquetando el nodo origen
Siguiendo las indicaciones del punto anterior, etiquetamos el nodo de origen A.
Como acabamos de comenzar el acumulado será 0 y como no existe nodo predecesor lo dejaremos en blanco y estaremos en la iteración cero.
Todo ello da como resultado la etiqueta [0,-](0)
Etiquetando la primera iteración
Continuamos etiquetando los nodos que están conectado al nodo A que ahora mismo es nuestro nodo permanente.
El nodo A está conectado al nodo B y al nodo D.
La etiqueta del nodo B sería [4,A](1).
La etiqueta del nodo D sería [6,A](1).
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso es el nodo B.
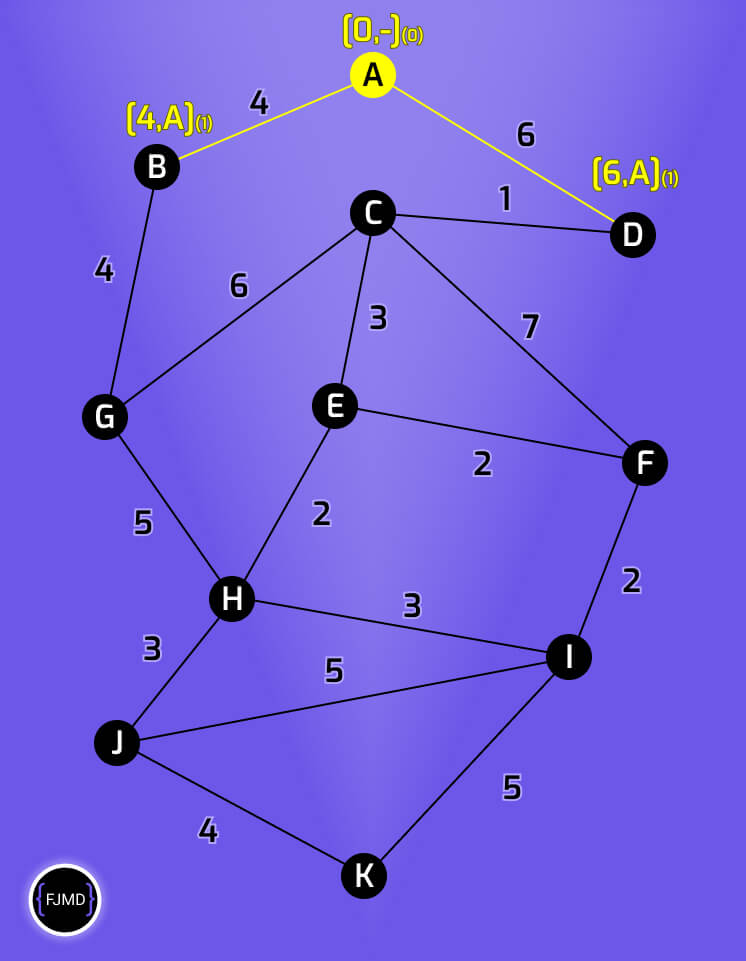
Etiquetando la segunda iteración
Como B sólo está conectado a G etiquetamos G obteniendo [8,B](2)
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso es el nodo D ya que su acumulado es de 6.
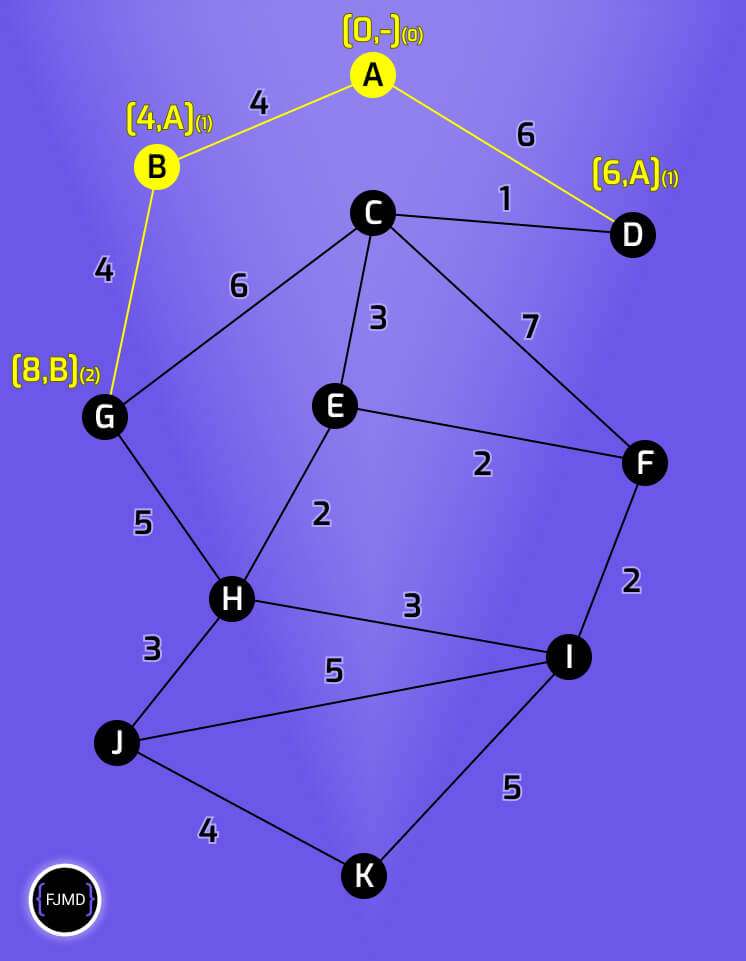
Etiquetando la tercera iteración
D está conectado sólo a C.
El nodo C tendrá la etiqueta [7,D](3)
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso, es el nodo C.
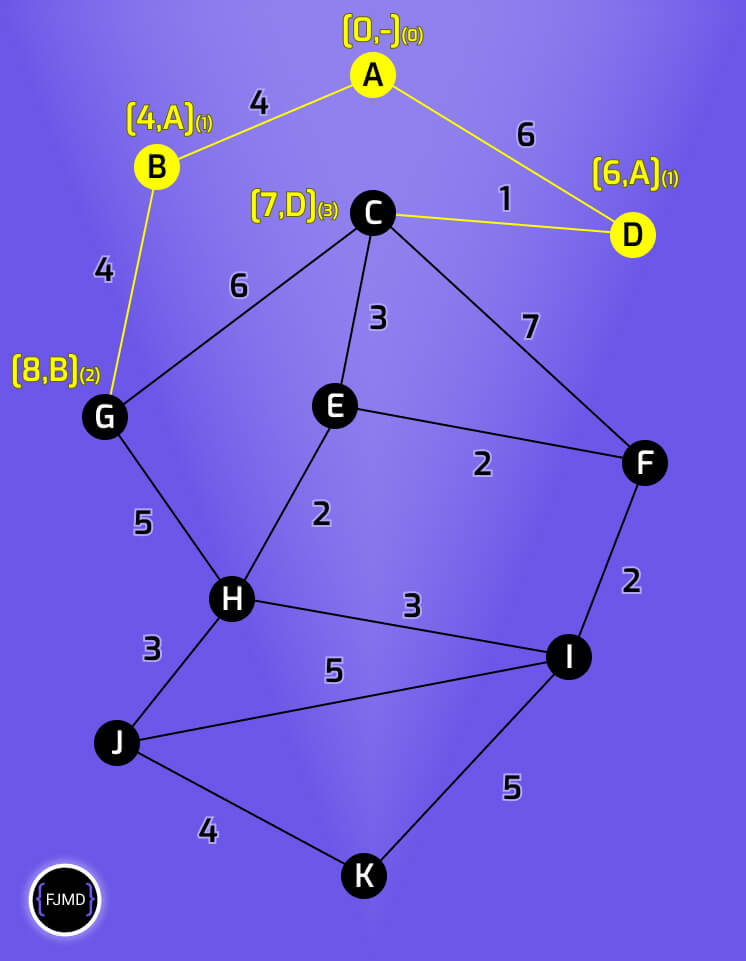
Etiquetando la cuarta iteración
C está conectado a G, E y F, así que pasamos a etiquetar.
El nodo G tendrá la etiqueta [13,C](4). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado, es decir, [8,B](2)
El nodo E tendrá la etiqueta [10,C](4)
El nodo F tendrá la etiqueta [14,C](4)
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso es el nodo G con un acumulado de 8.
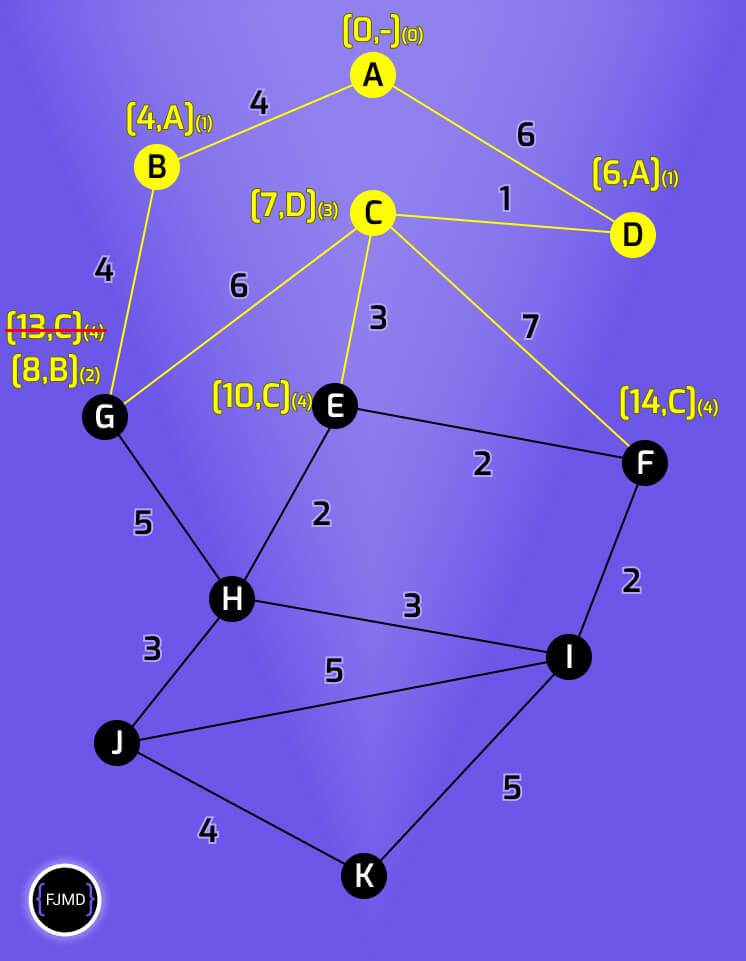
Etiquetando la quinta iteración
G sólo está conectado a H.
El nodo H tendrá la etiqueta [13,G](5)
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso es el nodo E con un acumulado de 10.
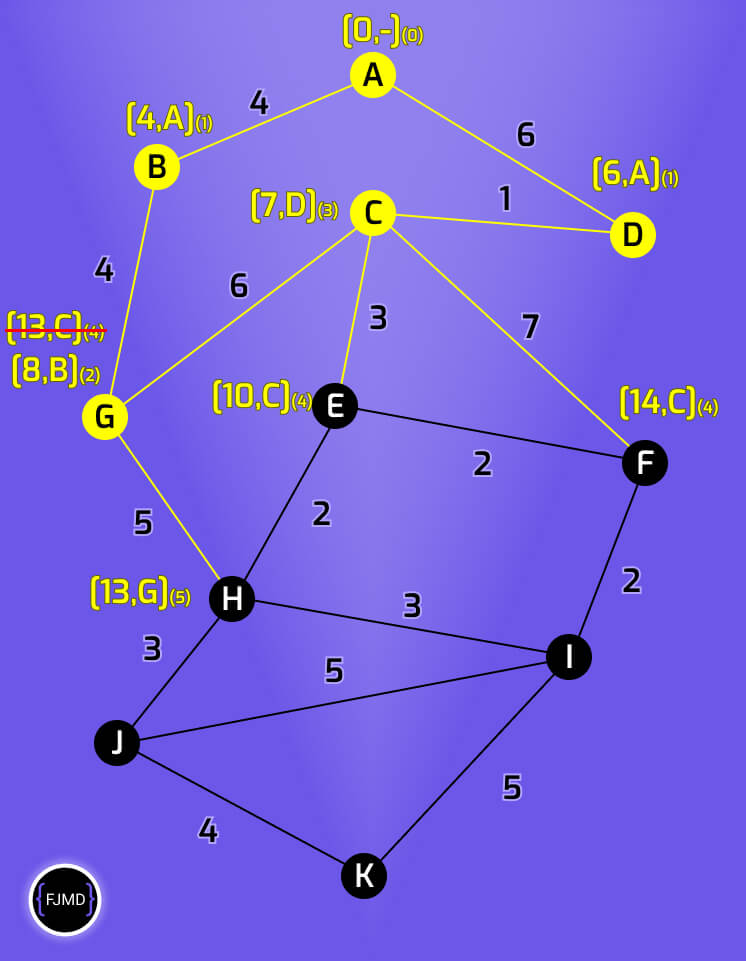
Etiquetando la sexta iteración
E está conectado a F y H, así que pasamos a etiquetar.
El nodo F tendrá la etiqueta [12,E](6). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado, que en este caso es la nueva etiqueta [12,E](6)
El nodo H tendrá la etiqueta [12,E](6). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado que, en este caso es la nueva etiqueta [12,E](6)
Elegimos como nodo permanente el nodo cuyo acumulado sea menor. En este caso, hay dos nodos con el mismo menor acumulado que son H y F así que escojo uno al azar como nodo permanente, por ejemplo el nodo F.
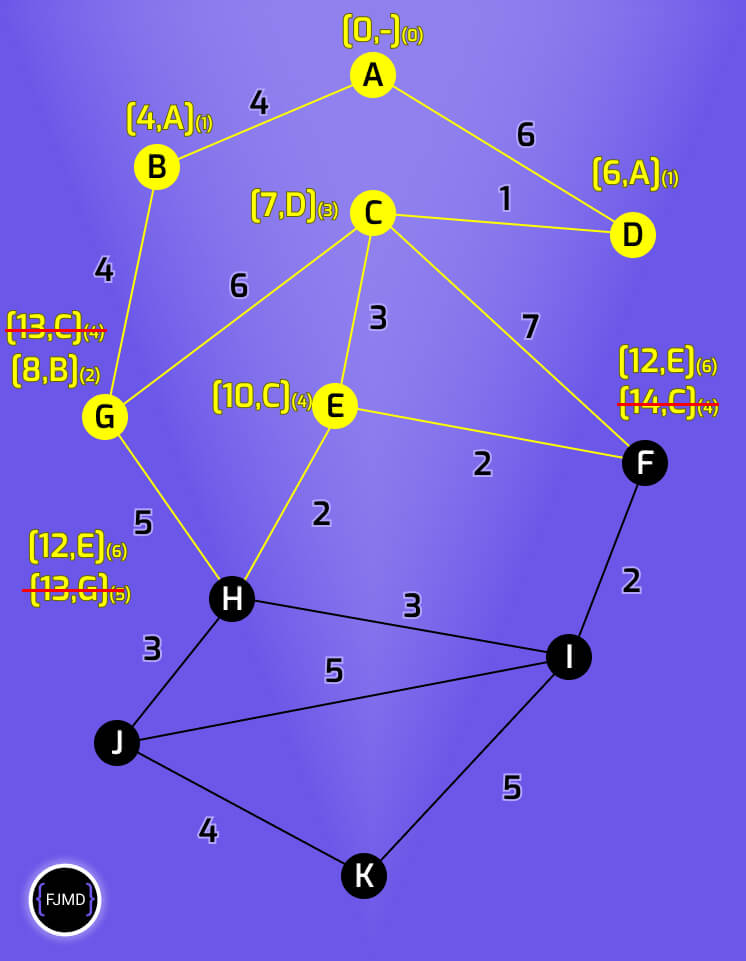
Etiquetando la séptima iteración
F sólo está conectado a I.
El nodo I tendrá la etiqueta [14,F](7)
Ahora elegimos como nodo permanente el nodo cuyo acumulado sea menor, que en este caso, es el nodo H con un acumulado de 12.

Etiquetando la octava iteración
H está conectado a I y J, así que pasamos a etiquetar.
El nodo I tendrá la etiqueta [15,H](8). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado que en este caso es la antigua etiqueta [14,F](7)
El nodo J tendrá la etiqueta [15,H](7).
Elegimos como nodo permanente el nodo cuyo acumulado sea menor que en este caso I con la etiqueta [14,F]7

Etiquetando la novena iteración
I está conectado a H, J y K, así que pasamos a etiquetar.
El nodo H tendrá la etiqueta [17,I](8). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado que en este caso es la antigua etiqueta [12,E](6)
El nodo J tendrá la etiqueta [19,I](8) pero al estar ya etiquetada un un acumulado menor me quedo con la etiqueta anterior [15,H](7).
Elegimos como nodo permanente el nodo cuyo acumulado sea menor que en este caso J con la etiqueta [15,H]7
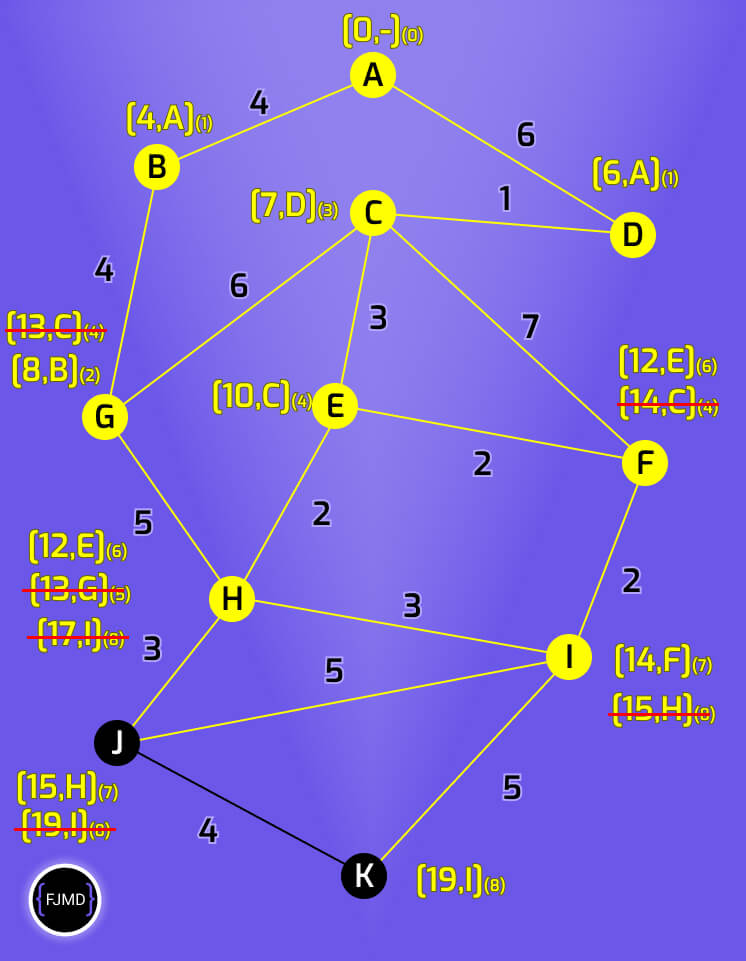
Etiquetando la décima iteración
J está conectado a H y K, así que pasamos a etiquetar.
El nodo H tendrá la etiqueta [18,J](9). Pero ojo, como ya tenía una etiqueta nos quedamos con la etiqueta de menor acumulado que en este caso es la antigua etiqueta [12,E](6)
El nodo K tendrá la etiqueta [19,J](9).
Ya hemos recorrido todos los nodos y hemos alcanzado el nodo destino K así que el algoritmo finaliza.
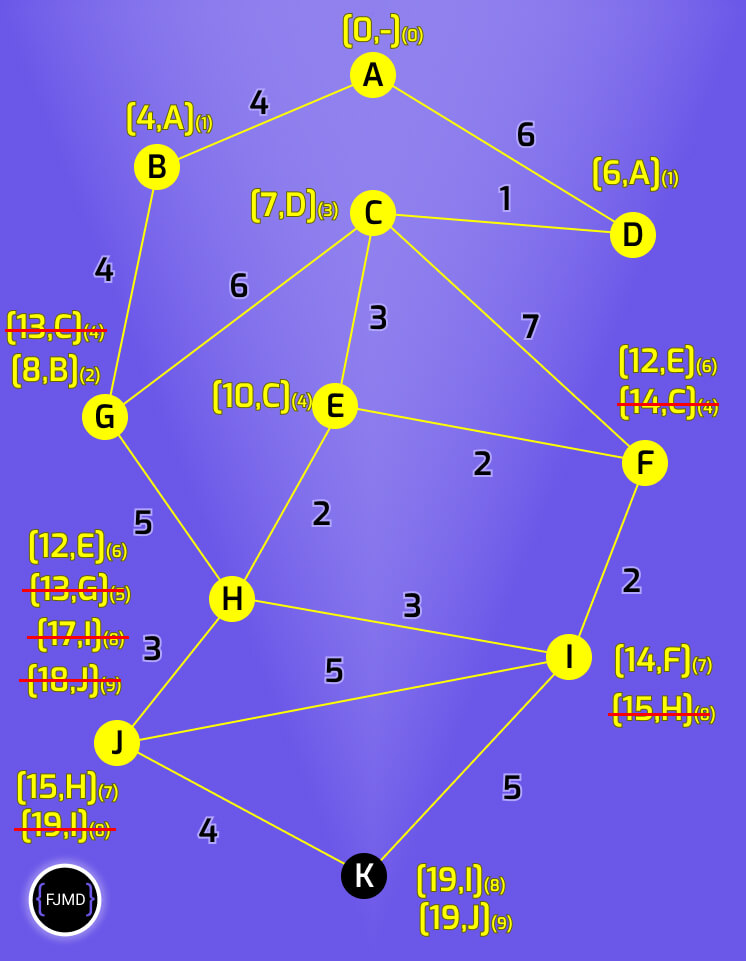
Obteniendo la ruta óptima
Según las etiquetas de K vemos que hay dos etiquetas con el mismo acumulado, eso significa que hay dos caminos óptimos.
Para obtener los caminos tan sólo hay que seleccionar una etiqueta e ir recorriendo los nodos el la dirección indicada.
Por ejemplo, imagina que elegimos la primera etiqueta [19,I](8), el recorrido sería:
- La etiqueta seleccionada de K [19,I](8) me indica ir a I
- La etiqueta de I [14,F](7) me indica ir a F
- La etiqueta de F [12,E](6) me indica ir a E
- La etiqueta de E [10,C](4) me indica ir a C
- La etiqueta de C [7,D](3) me indica ir a D
- La etiqueta de D [6,A](1) me indica ir a A que es mi origen.
Te dejo a ti dibujar la otra ruta óptima 🎉
Hasta luego 🖖



