¿Qué es un algoritmo genético 🤖🧬? Te lo cuento fácil 😉
Publicado el 22.01.2023 a las 23:43
¿Qué es un algoritmo genético 🤖🧬? Te lo cuento fácil 😉
⚫ ¿Qué es un algoritmo genético?
🟣 ¿Para qué se usan los algoritmos genéticos?
⚫ Un poco de genética
🟣 Selección natural
🟣 Reproducción
🟣 Mutación
⚫ ¿Cómo evoluciona el algoritmo genético?
⚫ Resolviendo el problema del comercial
🟣 Planteamiento
🟣 Inicialización de la población
🟣 Evaluación de la función de fitness
🟣 Selección
🟣 Cruce o reproducción
🟣 Mutación
🟣 Nueva población
⚫ Resumen
⚫ Calcular en vivo 🤖
⚫ Código fuente
¿Qué es un algoritmo genético 🤖🧬? Te lo cuento fácil 😉
¿Qué es un algoritmo genético?
Un algoritmo genético es un método computacional inspirado en el proceso evolutivo de los seres vivos.
A diferencia de los algoritmos tradicionales, que buscan una solución a través de un proceso lógico y sistemático, los algoritmos genéticos buscan una solución a través de la simulación de mecanismos de selección natural, reproducción y mutación.
Los algoritmos genéticos son algoritmos heurísticos, lo que significa que no garantizan encontrar la solución óptima, sino que buscan una solución "buena" en un tiempo razonable. Su capacidad de adaptarse a una gran variedad de problemas y su capacidad de buscar soluciones no triviales los hacen muy valiosos en una gran variedad de aplicaciones.
¿Para qué se usan los algoritmos genéticos?
Los algoritmos genéticos se utilizan para resolver problemas de optimización y aprendizaje automático, y se utilizan en:
- Planificación de rutas
- Diseño de circuitos
- Optimización de procesos
- Creación de modelos predictivos
- ...
Un poco de genética
Para entender cómo funciona un algoritmo genético, es importante comprender los conceptos fundamentales de la genética y la evolución.
En la naturaleza, los organismos tienen características heredadas de sus progenitores a través de los genes.
A través de la selección natural, los organismos con características que les dan una ventaja en su ambiente tienen más probabilidades de sobrevivir y reproducirse, pasando sus características a sus descendientes.
En un algoritmo genético, la solución a un problema se representa como un conjunto de "individuos" (también conocidos como "cromosomas", "poblaciones" o "soluciones").
Cada individuo tiene un conjunto de "genes" que representan una posible solución al problema. A través de la simulación de mecanismos de selección natural, reproducción y mutación, se busca una solución óptima al problema.
Selección natural
La selección natural es el resultado de la eliminación de los individuos más débiles y la supervivencia de los más fuertes que se dan en los seres vivos por factores ambientales.
En los algoritmos genéticos, la selección natural se simula mediante una función de "fitness" que evalúa la calidad de cada individuo.
Los individuos con mejores resultados en la función de fitness sobrevivirán y se reproducirán.
Reproducción
La reproducción en los seres vivos es el cruce de su material genético.
La reproducción en los algoritmos genéticos se simula mediante el "cruce" de los cromosomas o individuos o soluciones, donde se combinan los genes de dos individuos para crear un nuevo individuo.
Mutación
Una mutación es el cambio al azar en la secuencia de los genes de un ser vivo que produce una variación en las características de este. Se presenta de manera espontánea y súbita o por la acción de mutágenos.
La mutación en los algoritmos genéticos se simula mediante la introducción aleatoria de cambios en los genes de un individuo.
¿Cómo evoluciona el algoritmo genético?
El proceso de selección natural, después reproducción y por último mutación, se repetirán varias veces, generando una nueva generación de individuos en cada iteración.
A medida que se avanza a través de las generaciones, los individuos con mejores características tienden a dominar la población, y la función de fitness de la población en su conjunto tiende a aumentar.
El proceso finaliza cuando se alcanza una solución que cumple con un criterio de parada preestablecido o cuando se alcanza un cierto nivel de optimización.
Resolviendo el problema del comercial
Planteamiento
El problema del comercial o TSP, por sus siglas en inglés (Travelling Salesman Problem) es un problema donde un comercial o vendedor tiene que visitar n clientes o ciudades (nodos) y lo quiere hacer con el menor coste volviendo finalmente al punto de partida y sin repetir ningún cliente o ciudad.
El menor coste puede ser el menor tiempo, el menor número de kilómetros, el menos gasto económico (evitando peajes, puertos de montaña...)...
Cuando los clientes o ciudades a visitar son pocos es fácil resolver, pero a medida que aumenta el número de clientes a visitar se va complicando exponencialmente lo que implica que su solución es computacionalmente muy costosa.
Resolverlo por fuerza bruta para un gran número de nodos sería una locura.
El número de soluciones válidas es (n-1)!, el factorial del número de nodos (en este caso clientes o ciudades) menos uno.
A continuación te dejo una lista de cómo va evolucionando el número de soluciones en función al número de clientes a visitar:
- 2 clientes -> 1 solución
- 3 clientes -> 2 soluciones
- 4 clientes -> 6 soluciones
- 5 clientes -> 24 soluciones
- 6 clientes -> 120 soluciones
- 7 clientes -> 720 soluciones
- 8 clientes -> 5.040 soluciones
- 9 clientes -> 40.320 soluciones
- ...
- 20 clientes -> 2.432.902.008.176.640.000 soluciones
- ...
Bueno, vamos al lío, supongamos que queremos visitar 9 clientes, una representación gráfica podría ser el siguiente grafo 👇
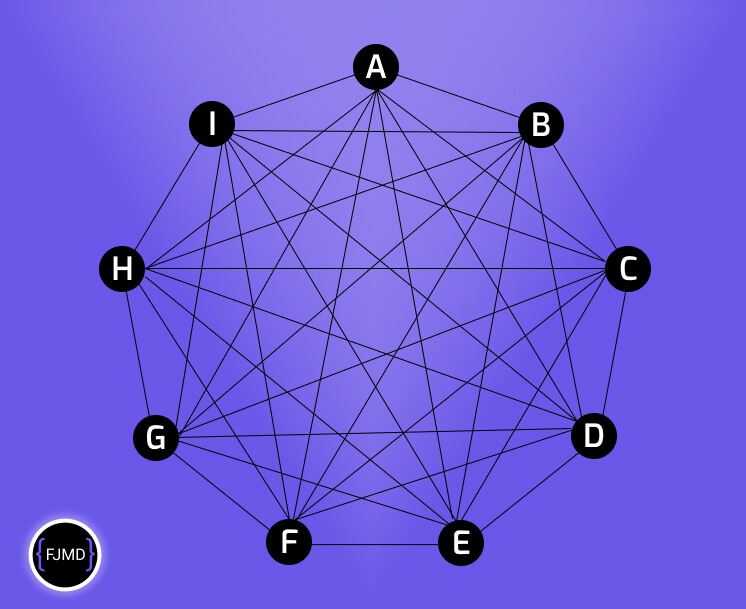
Las longitudes de las líneas no son proporcionales a su costo, es una manera que he tenido de representarlo gráficamente para que lo veas claro.
Recuerda que el costo puede ser el número de kilómetros, el tiempo que se tarda en recorrer el camino entre dos nodos o el coste económico de la ruta (peajes, más consumo extra por subidas de puertos de montaña...)
Para no complicar la representación gráfica con el coste de cada recorrido, voy a poner en una matriz el coste que hay entre cada uno de los nodos (clientes o ciudades):
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| A | - | 4 | 6 | 2 | 8 | 5 | 2 | 3 | 7 |
| B | 4 | - | 4 | 1 | 8 | 8 | 2 | 4 | 5 |
| C | 6 | 4 | - | 4 | 9 | 4 | 6 | 5 | 1 |
| D | 2 | 1 | 4 | - | 4 | 1 | 2 | 1 | 8 |
| E | 8 | 8 | 9 | 4 | - | 7 | 5 | 1 | 6 |
| F | 5 | 8 | 4 | 1 | 7 | - | 7 | 2 | 8 |
| G | 2 | 2 | 6 | 2 | 5 | 7 | - | 4 | 2 |
| H | 3 | 4 | 5 | 1 | 1 | 2 | 4 | - | 8 |
| I | 7 | 5 | 1 | 8 | 6 | 8 | 2 | 8 | - |
Inicialización de la población
Creamos una población inicial de soluciones al problema. Las creamos de forma aleatoria.
Para generar la población inicial usaré un array origen que serán todos los nodos (A, B...) y generaré un número aleatorio entre 0 y la longitud del array de origen, el resultado será el índice del elemento que extraeré del array origen y lo añado en un nuevo array solución, así hasta que el array origen que vacío.
Cada solución se representa mediante un "cromosoma", que es una secuencia de ciudades o clientes en la que se recorren.
Genero una población inicial con 9 cromosomas
["A", "I", "E", "H", "B", "C", "F", "G", "D", "A"] //CROMOSOMA 1
["A", "H", "F", "B", "G", "E", "D", "I", "C", "A"] //CROMOSOMA 2
["A", "E", "H", "B", "G", "D", "C", "I", "F", "A"] //CROMOSOMA 3
["A", "E", "F", "I", "C", "B", "G", "H", "D", "A"] //CROMOSOMA 4
["A", "F", "I", "G", "C", "E", "B", "H", "D", "A"] //CROMOSOMA 5
["A", "G", "E", "C", "F", "H", "D", "I", "B", "A"] //CROMOSOMA 6
["A", "D", "C", "I", "F", "B", "E", "G", "H", "A"] //CROMOSOMA 7
["A", "H", "E", "D", "F", "I", "B", "C", "G", "A"] //CROMOSOMA 8
["A", "F", "D", "H", "G", "C", "E", "I", "B", "A"] //CROMOSOMA 9
Evaluación de la función de fitness
Evaluamos la calidad de cada solución o cromosoma mediante una función de fitness, que mide la longitud del recorrido.
Para el cromosoma o solución 1, recordemos ["A", "I", "E", "H", "B", "C", "F", "G", "D", "A"], el recorrido será:
- Ir de A a I = 7
- Ir de I a E = 6
- Ir de E a H = 1
- Ir de H a B = 4
- Ir de B a C = 4
- Ir de C a F = 4
- Ir de F a G = 7
- Ir de G a D = 2
- Ir de D a A = 2
En total tenemos que el cromosoma o solución 1 tiene un coste de 7 + 6 + 1 + 4 + 4 + 4 + 7 + 2 + 2 = 37
Hacemos lo mismo para todos los cromosomas o soluciones:
- Solución 1 - coste 37
- Solución 2 - coste 39
- Solución 3 - coste 35
- Solución 4 - coste 37
- Solución 5 - coste 45
- Solución 6 - coste 40
- Solución 7 - coste 43
- Solución 8 - coste 34
- Solución 9 - coste 41
Selección
Se seleccionan los individuos con la mejor solución de la función de fitness para reproducirse y crear una nueva generación.
En nuestro caso seleccionaremos las soluciones que arrojan un menor valor de coste, que son la solución 3 y 8
- Solución 1 - longitud 37
- Solución 2 - longitud 39
- Solución 3 - longitud 35 👈
- Solución 4 - longitud 37
- Solución 5 - longitud 45
- Solución 6 - longitud 40
- Solución 7 - longitud 43
- Solución 8 - longitud 34 👈
- Solución 9 - longitud 41
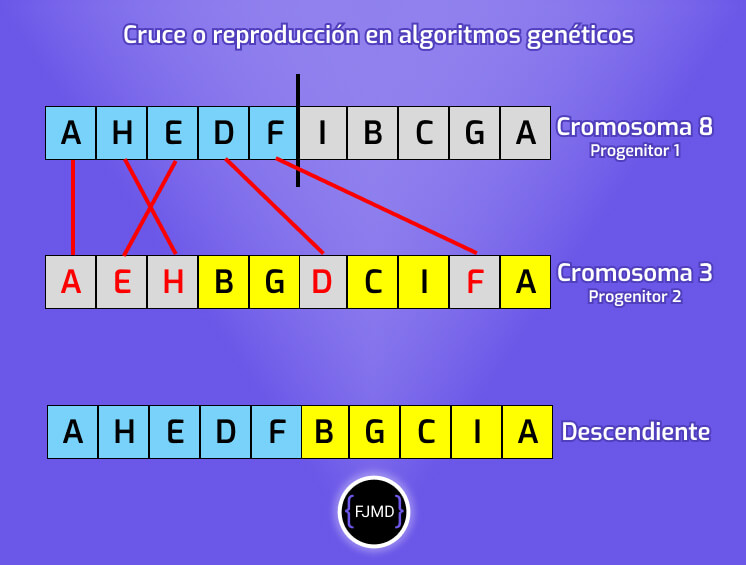
Cruce o reproducción
Se combinan los genes de los dos individuos seleccionados para crear un nuevo cromosoma.
Hemos dicho que los individuos seleccionados son, el mejor que es el cromosoma 8 y el segundo mejor que es el cromosoma 3:
El cromosoma o solución 8
| A | H | E | D | F | I | B | C | G | A |
|---|
El cromosoma o solución 3
| A | E | H | B | G | D | C | I | F | A |
|---|
Elegimos un lugar aleatorio para romper el cromosoma 8, por ejemplo en su posición 5 y nos quedaremos con su primera parte.
| A | H | E | D | F | I | B | C | G | A |
|---|
Para completar el cromosoma, eliminaremos del cromosoma 3 los nodos, genes o ciudades que ya están seleccionados de la primera mitad del cromosoma 8, es decir, eliminaremos del cromosoma 3 a A, H, E, D y F y los genes restantes serán los que complementarán nuestro cromosoma solución.
| A | E | H | B | G | D | C | I | F | A |
|---|
Y obtenemos como resultado nuestro nuevo cromosoma:
| A | H | E | D | F | B | G | C | I | A |
|---|
Mutación
Se introducen cambios aleatorios en los genes de algunos individuos para introducir variabilidad en la población.
Por ejemplo, cambiamos la posición 2 por la 7
| A | H | E | D | F | B | G | C | I | A |
|---|
Obteniendo, por fin, nuestro nuevo cromosoma:
| A | G | E | D | F | B | H | C | I | A |
|---|

Nueva población
Para obtener la nueva población lo que hacemos es sustituir el cromosoma que daba peor resultado de la población inicial por el nuevo cromosoma obtenido.
Si recordamos, el peor cromosoma de la población inicial era el cromosoma 5 que tenía un costo de 45, lo sustituimos por nuestro nuevo cromosoma, obteniendo nuestra nueva población.
["A", "I", "E", "H", "B", "C", "F", "G", "D", "A"] //CROMOSOMA 1
["A", "H", "F", "B", "G", "E", "D", "I", "C", "A"] //CROMOSOMA 2
["A", "E", "H", "B", "G", "D", "C", "I", "F", "A"] //CROMOSOMA 3
["A", "E", "F", "I", "C", "B", "G", "H", "D", "A"] //CROMOSOMA 4
["A", "G", "E", "D", "F", "B", "H", "C", "I", "A"] //NUEVO CROMOSOMA 👈
["A", "G", "E", "C", "F", "H", "D", "I", "B", "A"] //CROMOSOMA 6
["A", "D", "C", "I", "F", "B", "E", "G", "H", "A"] //CROMOSOMA 7
["A", "H", "E", "D", "F", "I", "B", "C", "G", "A"] //CROMOSOMA 8
["A", "F", "D", "H", "G", "C", "E", "I", "B", "A"] //CROMOSOMA 9
Ahora sometemos a esta nueva población a todo el proceso por el cual la hemos obtenido:
- Evaluación de la función fitness
- Selección
- Cruce
- Mutación
- Nueva población
El proceso finaliza cuando se alcanza un criterio de parada preestablecido, como un número específico de generaciones o cuando se alcanza un cierto nivel de optimización.
En este ejemplo voy a parar el algoritmo cuando realize 10.000 iteraciones obteniendo que la mejor solución tendría un coste de 21 🎉
Si dibujo en rojo el camino con menos costo sobre el grafo inicial quedaría:

Resumen
En resumen, los algoritmos genéticos son una técnica computacional inspirada en la evolución de los seres vivos, que permite buscar soluciones óptimas a problemas de optimización y aprendizaje automático.
Calcular en vivo 🤖
A continuación te dejo el programa en vivo que ejectua el algoritmo para que puedas ver cómo se alcanza la mejor solución al problema.
Cuando pulses en el botón Inicia, se comenzará el cálculo, haciéndose una iteración cada medio segundo para que de tiempo a ver cómo evoluciona. Cuando se llegue a la iteración número 100 se parará.
Puedes cambiar los milisegundos entre iteración si lo deseas entre 100 y 5000 ms.
Podrás iniciar el programa tanta veces como quieras.
Ten en cuenta que como cada vez que se inicia se calcula una población inicial aleatoria es posible que finalizadas las 100 iteraciones no se encuentre la mejor solución o cromosoma que es la que devuelve un fitness de 21.
En verde verás el cromosoma con mejor fitness y en azul verás el segundo mejor cromosoma y serán los que se reproduzcan o se crucen.
| Cromosomas (individuos o soluciones) | Fitness | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | E | G | D | B | H | I | F | C | A | 46 |
| A | D | G | C | E | B | F | H | I | A | 52 |
| A | C | D | I | G | F | H | B | E | A | 49 |
| A | I | D | C | G | F | B | H | E | A | 53 |
| A | B | H | C | G | F | E | I | D | A | 49 |
| A | H | F | I | E | D | B | G | C | A | 38 |
| A | D | G | H | C | B | F | E | I | A | 45 |
| A | B | G | H | D | C | I | F | E | A | 39 |
| A | E | F | C | D | H | G | I | B | A | 39 |
Código fuente
Al código se le podrían realizar varias refactorizaciones, pero este artículo ya me ha consumido más tiempo del que tenía previsto 😅
//deno run --watch src/app/pages/blog/articles/genetic-algorithm/code.ts
const nodes: string[] = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
const costs: number[][] = [
[0, 4, 6, 2, 8, 5, 2, 3, 7],
[4, 0, 4, 1, 8, 8, 2, 4, 5],
[6, 4, 0, 4, 9, 4, 6, 5, 1],
[2, 1, 4, 0, 4, 1, 2, 1, 8],
[8, 8, 9, 4, 0, 7, 5, 1, 6],
[5, 8, 4, 1, 7, 0, 7, 2, 8],
[2, 2, 6, 2, 5, 7, 0, 4, 2],
[3, 4, 5, 1, 1, 2, 4, 0, 8],
[7, 5, 1, 8, 6, 8, 2, 8, 0],
];
const initialPopulation:string[][] = toGenerateInitialPopulation(9);
/* const initialPopulation:string[][] = [
['A', 'I', 'E', 'H', 'B', 'C', 'F', 'G', 'D', 'A'],
['A', 'H', 'F', 'B', 'G', 'E', 'D', 'I', 'C', 'A'],
['A', 'E', 'H', 'B', 'G', 'D', 'C', 'I', 'F', 'A'],
['A', 'E', 'F', 'I', 'C', 'B', 'G', 'H', 'D', 'A'],
['A', 'F', 'I', 'G', 'C', 'E', 'B', 'H', 'D', 'A'],
['A', 'G', 'E', 'C', 'F', 'H', 'D', 'I', 'B', 'A'],
['A', 'D', 'C', 'I', 'F', 'B', 'E', 'G', 'H', 'A'],
['A', 'H', 'E', 'D', 'F', 'I', 'B', 'C', 'G', 'A'],
['A', 'F', 'D', 'H', 'G', 'C', 'E', 'I', 'B', 'A'],
]; */
const solutionMap:Map<string,string> = new Map<string, string>();
solutionMap.set('A', '0');
solutionMap.set('B', '1');
solutionMap.set('C', '2');
solutionMap.set('D', '3');
solutionMap.set('E', '4');
solutionMap.set('F', '5');
solutionMap.set('G', '6');
solutionMap.set('H', '7');
solutionMap.set('I', '8');
solutionMap.set('0', 'A');
solutionMap.set('1', 'B');
solutionMap.set('2', 'C');
solutionMap.set('3', 'D');
solutionMap.set('4', 'E');
solutionMap.set('5', 'F');
solutionMap.set('6', 'G');
solutionMap.set('7', 'H');
solutionMap.set('8', 'I');
function getTwoBestSolutions(population: string[][]): string[][] {
const mapFitnesSolution = getMapFitnesSolution(population);
const mapSorted = new Map(
[...mapFitnesSolution].sort((a, b) => {
// Para comparar las keys 👉 a[0] b[0]
// Para comparar los valores 👉 a[1] b[1]
return a[1] - b[1];
})
);
const firstBestSolutionIndex = [...mapSorted][0][0]; //así cojo el index
const secondBestSolutionIndex = [...mapSorted][1][0];
return [
population[firstBestSolutionIndex],
population[secondBestSolutionIndex],
];
}
function chromosomeCrossover(twoBestChromosme: string[][]):string[]{
const splitBy=getRandomNumber(2,twoBestChromosme[0].length-1);
const startChromosmeSolution=twoBestChromosme[0].slice(0,splitBy);
let endChromosmeSolution:string[]=[...twoBestChromosme[1]];
startChromosmeSolution.forEach(geneOK=>{
const index = endChromosmeSolution.indexOf(geneOK);
if(index===-1) console.log('¡Algo no va bien!');
endChromosmeSolution.splice(index,1);
})
const exit =startChromosmeSolution.concat(endChromosmeSolution)
return exit;
}
function getMutation(chromosome:string[]):string[]{
const firstIndex=getRandomNumber(1,chromosome.length-2); //así evito que me pille el índice 0 o el último índice, ya que esos tienen que ser siempre el nodo A
const secondIndex=getRandomNumber(1,chromosome.length-2);
if(firstIndex===secondIndex) return chromosome;
const changeOne=chromosome[firstIndex];
const changeTwo=chromosome[secondIndex];
chromosome[firstIndex]=changeTwo;
chromosome[secondIndex]=changeOne;
return chromosome;
}
function getWorstSolution(population: string[][]): string[] {
const mapFitnesSolution = getMapFitnesSolution(population);
const mapSorted = new Map(
[...mapFitnesSolution].sort((a, b) => {
return a[1] - b[1]; // Some sort function comparing keys with a[0] b[0] or values with a[1] b[1]
})
);
const worstSolutionIndex = [...mapSorted][population.length-1][0]; //así cojo el index
return population[worstSolutionIndex];
}
function getMapFitnesSolution(population: string[][]): Map<number, number> {
const fitnesSolutionMap = new Map<number, number>();
population.forEach((solution, index) => {
fitnesSolutionMap.set(index, getFitness(solution));
});
return fitnesSolutionMap;
}
function getFitness(chromose: string[]): number {
let result: number = 0;
for (let i = 0; i < chromose.length - 1; i++) {
const row: number = Number(solutionMap.get(chromose[i])) || 0;
const column: number = Number(solutionMap.get(chromose[i + 1])) || 0;
const cost = costs[row][column];
result += cost;
}
return result;
}
function toGenerateInitialPopulation(numberOfChromosomes: number): string[][] {
const chromosomes: string[][] = [];
for (let i = 0; i < numberOfChromosomes; i++) {
const initialArray = nodes.slice(1, nodes.length);
const finalArray = [];
while (initialArray.length > 0) {
const index = getRandomNumber(0, initialArray.length - 1);
finalArray.push(initialArray[index]);
initialArray.splice(index, 1);
}
finalArray.unshift('A');
finalArray.push('A');
chromosomes.push(finalArray);
}
return chromosomes;
}
function getNewPopulation(population:string[][],newChromosome:string[]):string[][]{
const worstChromosome=getWorstSolution(population);
const indexWorstChromosome=population.indexOf(worstChromosome);
if(indexWorstChromosome===-1){
console.log('Algo no va bien');
return population
}
population[indexWorstChromosome]=newChromosome;
return population;
}
function getRandomNumber(min: number, max: number): number {
return Number((Math.random() * (max - min) + min).toFixed(0));
}
let population=[...initialPopulation];
for(let i=0;i<10000;i++){
const twoBestChromoses=getTwoBestSolutions(population);
const crossover=chromosomeCrossover(twoBestChromoses);
const mutation = getMutation(crossover);
population=getNewPopulation(population,mutation);
}
const bestChromosome=getTwoBestSolutions(population)[0];
console.log('Mejor cromosoma: ', bestChromosome, 'Fitness: ', getFitness(bestChromosome));
Hasta luego 🖖